Data access methods need to modified or newly invented to adapt with ever changing workload requirements and hardware changes. This paper looks at the challenges in designing new access methods which increasingly needs to be application and hardware aware. The fundamental challenges faced are to minimize a) Read time - R b) Update cost - U c) memory over head - M and the conjecture made is that when optimizing the read-update-memory (RUM) overheads, optimizing in any two negatively impacts the third. Deciding which overheads to optimize for and to what extend has always been and remains the prominent part of designing access methods.
RUM Overheads
Access methods enable us to read or write base data potentially using auxiliary data such as indexes to provide performance improvement.
Read Overhead
RO is the read amplification which is the ratio between the total amount of data read including auxiliary data and base data, divided by the amount of data read.
Update Overhead
UO is the write amplification which is the ratio between the size of physical update performed for one logical update divided by the size of the logical update. A logical update can involve multiple physical updates for e.g. update to base data and auxiliary data like indexes
Memory Overhead
MO is the space amplification which is the ratio between the space utilized for auxiliary and base data, divided by the space utilized for base data.
The theoretical minimum for overhead is to have the ratio equal to 1.0 which implies that the base data is always read and updated directly and no extra bit of memory is wasted. Achieving these bounds for all the three overheads simultaneously is not possible as there is always price to pay for every optimization. When designing an access method all the three overheads should be minimal but depending on the application workload and available technology they need to prioritized.
RUM Conjecture
designing access methods that set an upper bound for two of the RUM overheads, leads to a hard lower bound for the third overhead which cannot be further reduced
In other words, we can choose which two overheads to prioritize and optimize for and pay the price by having the third overhead greater than the hard lower bound. The following figure shows some popular access methods mapped to three dimensional RUM space projected on a two dimensional plane.
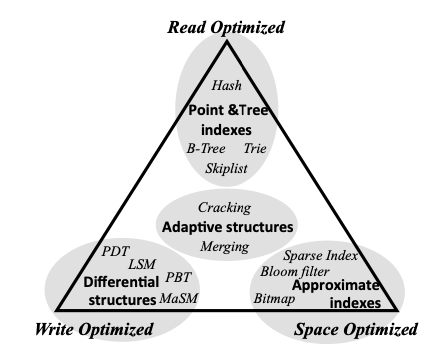
Using the RUM space we can understand the current access methods interms of which overhead they prioritize and can choose the appropriate one that suits the need. It also helps in designing new access methods or a combination of access methods which can tune based on available technology and dynamically adapt to new workloads and hence covering the RUM space in aggregate.